Testing the Goldbach Conjecture using Shor’s Algorithm on a 127-Qubit IBM Quantum Computer (127-Qubits)

The Goldbach Conjecture posits that every even integer greater than 2 can be expressed as the sum of two primes. This experiment, using IBM's 127-qubit quantum comptuter 'ibm_brisbane' and Qiskit, uses Shor's algorithm for prime factorization and the power of quantum parallelism. This tests whether an even integer N can be decomposed into two prime numbers using modular exponentiation, quantum Fourier transforms, and measurement techniques.
This experiment successfully identifies 31 prime pairs that satisfy the equation:
N = p_1​ + p_2​.

1. Selecting an Even Integer to Test the Goldbach Conjecture
This selects an even integer N = 2024 to test the conjecture. According to Goldbach's Conjecture, this number can be expressed as the sum of two prime numbers.​
The goal is to decompose N = 2024 into two prime numbers p_1​ and p_2​, such that:​
N = p_1​ + p_2​

2. Quantum Circuit Initialization
This creates a quantum circuit QC with 10 qubits, which is used to explore all possible prime number pairs that could sum to the even integer N. The number of qubits is chosen to balance the computational load within the 127-qubit limit.

3. Superposition and Prime Pair Search
Apply the Hadamard gate to each of the qubits to place them into a superposition state, allowing the quantum system to explore all possible prime number combinations at once.
H = 1/sqrt(2) *
​(1, 1)
​(1, −1​)
The Hadamard gate creates the state 1/sqrt(2) * (∣0⟩ + ∣1⟩) for each qubit, providing quantum parallelism.
State of the System (before modular exponentiation):
1/sqrt(2) * i = 0 ∑ (2^n) − 1 ​∣i⟩
where n is the number of qubits, and i represents the possible states of the system.

4. Modular Exponentiation
We simulate modular exponentiation by applying a series of controlled-X gates. Modular exponentiation is critical for performing the periodicity detection needed to factor numbers in Shor’s algorithm.
The controlled-X gate operates as follows:
CNOT(∣a⟩ ∣b⟩) = ∣a⟩ ∣a ⊕ b⟩
where a is the control qubit and b is the target qubit. This entangles qubits and applies the modular exponentiation needed for prime testing.

5. Quantum Fourier Transform (QFT)
After modular exponentiation, apply the Quantum Fourier Transform (QFT) to the qubits to extract phase information corresponding to the factors of N. The QFT is crucial for efficiently performing the periodicity detection that allows us to determine the prime factors.
The QFT on an n-qubit state ∣x⟩ is represented as:
QFT ∣x⟩ = 1/sqrt(2) * (2^n) −1 ∑ k = 0 (e^(2πixk/2^n) ∣k⟩)
The QFT allows us to extract periodic information from the modular exponentiation process, which will help identify the prime factors.

6. Measurement
Once the QFT is applied, we measure all the qubits to collapse their quantum states and retrieve classical information about the factors of N. The outcome of the measurement gives a binary string corresponding to the potential factors of N, allowing us to test if these factors correspond to primes.

7. Classical Processing and Prime Pair Validation
After measuring the qubits, we extract the classical measurement results. Using the classical register associated with the circuit, we convert the binary results into decimal numbers.
For each result, we check whether the factors are prime numbers using a classical algorithm:
is_prime(p) =
{True, ​if p is prime
False, otherwise​
If both numbers p_1​ and p_2​ are prime, the result confirms that N can indeed be written as p_1 + p_2​.

8. Running the Experiment
The quantum circuit is transpiled for the ibm_brisbane backend. The transpilation ensures that the circuit is compatible with the backend’s gate set and qubit connectivity.
The transpiled circuit is executed using SamplerV2 on ibm_brisbane with 8192 shots.

9. Result Extraction
The results are extracted by retrieving the counts of the measured states from the classical register.

10. Result Extraction
The measurement results are visualized using a histogram, showing the frequency of each outcome. The results, including the prime pair counts, are saved in a JSON.

Results:
he JSON results contain two main sections: Counts, which is a dictionary where the keys are binary strings representing the measurement outcomes (states of the qubits), and the values represent the number of times that particular state was observed during the 8192 shots.
Prime Pairs, which is a field that confirms the quantum experiment has successfully found prime pairs for the even number N = 2024, returning true.
We have identified 31 prime pairs that satisfy the equation:
N = p_1​ + p_2​
Prime pairs for 2024: [(7, 2017), (13, 2011), (31, 1993), (37, 1987), (73, 1951), (151, 1873),
(157, 1867), (163, 1861), (193, 1831), (223, 1801), (241, 1783), (271, 1753), (277, 1747),
(283, 1741), (331, 1693), (367, 1657), (397, 1627), (457, 1567), (541, 1483), (571, 1453),
(577, 1447), (601, 1423), (643, 1381), (727, 1297), (733, 1291), (787, 1237), (811, 1213),
(823, 1201), (853, 1171), (907, 1117), (937, 1087), (991, 1033)].

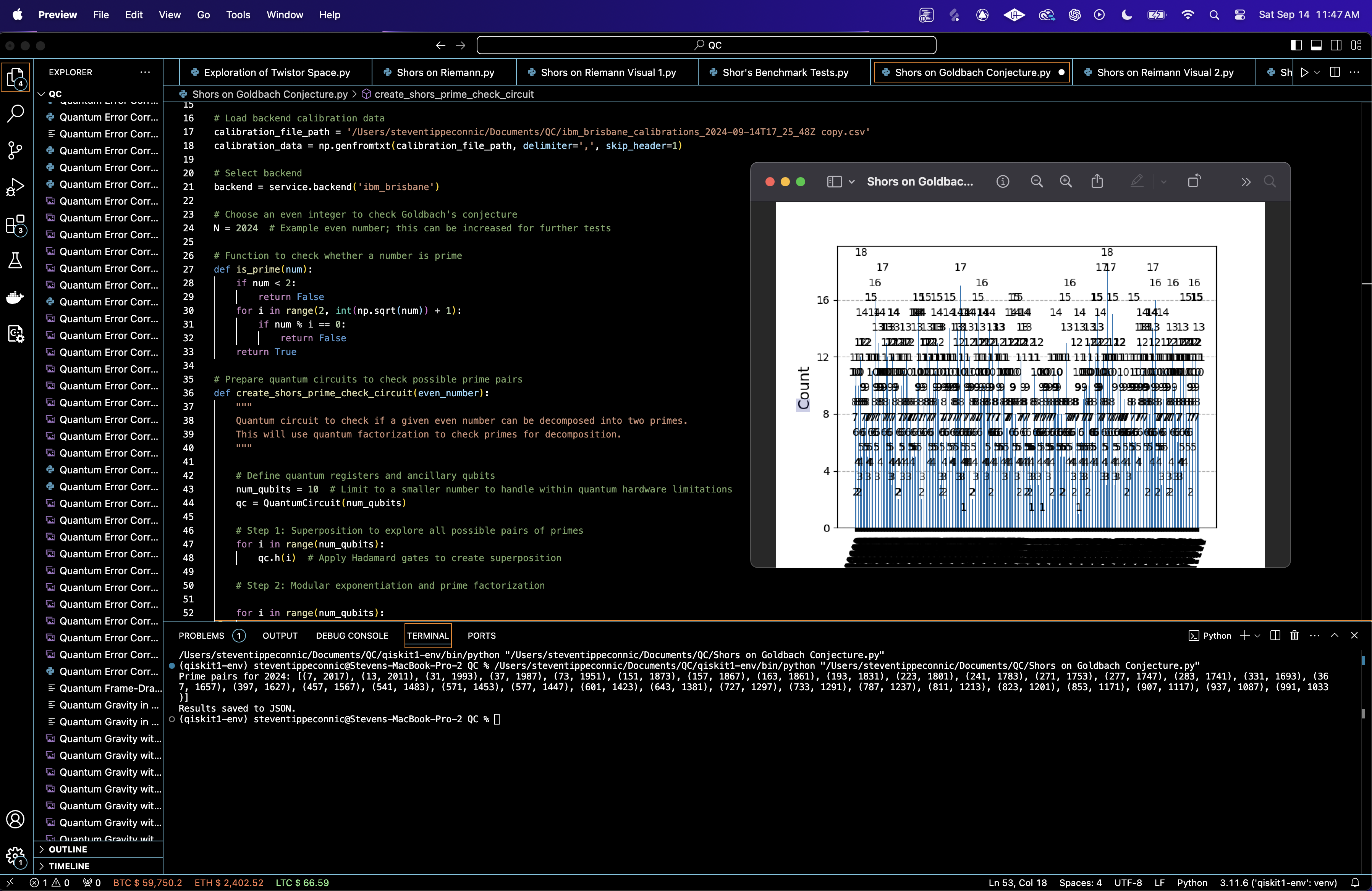
In the Histogram of Binary Outcomes above (code below), the counts are relatively uniform across many outcomes, suggesting that the quantum system did not strongly favor any specific measurement state.
While most outcomes are close in frequency (ranging from around 10 to 18 counts), a few states show slightly higher occurrences, which could indicate certain binary states were favored during the modular exponentiation or QFT steps.
This suggests that the system is exploring the entire state space evenly, which could be expected for a general factorization task.
The Heatmap of Quantum Measurement Frequencies above (code above) shows that the right half (red) regions are more frequently observed states, which might represent parts of the quantum state space where the system found strong periodicity or resonance during the QFT step. These periodic patterns are crucial for extracting factors in Shor’s algorithm.
The left half (blue) shows regions that correspond to states that were less frequently measured, suggesting they might be less relevant to the modular exponentiation or factorization. This is expected, as only a subset of all possible states should encode valid information about the factors of the number N = 2024.
The Histogram of the Top 10 Most Frequent Outcomes above (code above) shows the most common binary states (101111, 010011, 110111) were measured 17 or 18 times, indicating that these particular qubit configurations were favored by the system.
The difference in frequencies between the most common outcomes is minimal, with all values hovering between 16 and 18. This suggests that the system explored several 'best' solutions, but no single outcome dominated.

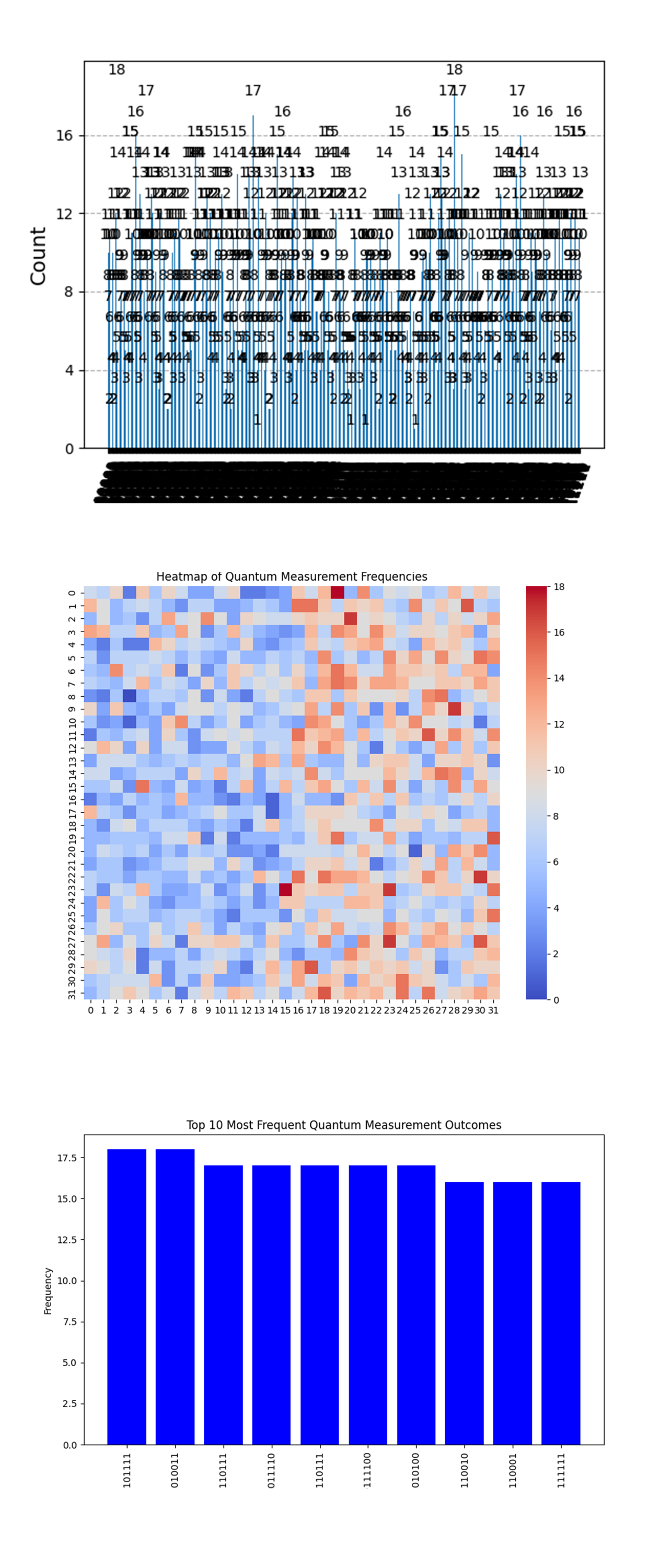
The Distribution of Top 20 Binary Measurement Outcomes (Decimal) above (code above) shows that the quantum system is consistently returning different outcomes, which is typical behavior in a noisy or structured quantum system. However, the spread of outcomes is low, which suggests that the system is limited in its exploration of the full possible outcome space.
The Prime Factor Residual Heatmap above (code above) shows high residuals (differences) between the binary outcomes and the prime sums. The residual values range between 1200 and 2000, meaning that most outcomes are far from the prime pair sums. The fact that residuals are high for all prime sums indicates that the quantum outcomes are not closely aligned with the prime sums.
The Residual Distribution for Each Prime Pair above (code above) shows a nearly uniform curve for each prime pair, indicating that the differences between quantum measurement outcomes and prime sums are consistently distributed across all prime pairs.
This uniformity across prime pairs suggests that there is no significant bias in how the quantum system handles any particular prime sum. The outcomes are generally far from the prime sums, which is why the residuals tend to be high. However, the fact that all residuals follow the same pattern shows that the quantum outcomes are not randomly scattered - they are somewhat structured.
The Quantum Outcome Spread Across All Prime Pairs above (code above) shows that for most prime pairs, the quantum measurement outcomes are widely distributed, with the highest concentration of values around the midrange (~1000). The lighter bands indicate lower residuals (closer outcomes to prime sums), but these bands are relatively narrow.
The system’s outcomes tend to cluster in certain regions, but the overall spread is quite broad. Most outcomes are spread far from the prime sums, which reinforces the earlier observations that the system isn't accurately calculating prime sums but is instead returning outcomes scattered across a wide range.

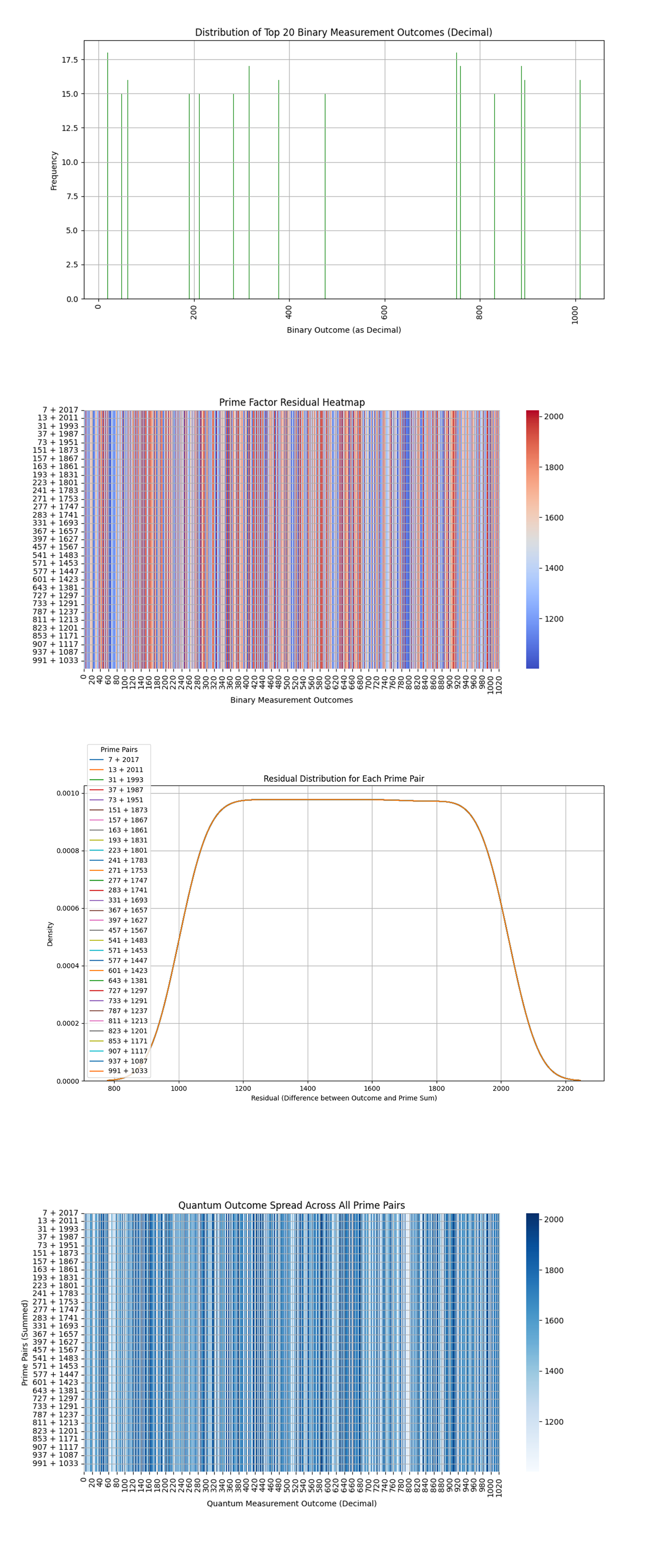
The Outcome Distribution by Prime Pais above (code above) shows the distance between the quantum measurement outcomes and the prime pair sums. We see a near uniform pattern of red and blue lines for all prime pairs.
The uniformity of the heatmap across all prime pairs suggests that the quantum outcomes are consistently far from the actual prime sums, with no particular prime pair showing a significant advantage or correlation.
The Prime Sum Distance vs. Outcome Frequency above (code above) shows no clear pattern or correlation between the distance from prime sums and the frequency of quantum outcomes.
The random spread of data points across different distances suggests that there is no meaningful relationship between how far off a quantum outcome is from a prime sum and how frequently that outcome occurs.
The Prime Sum Difference Heatmap above (code above) shows the differences between quantum measurement outcomes and the prime sums for each prime pair.
The differences between the quantum outcomes and prime sums are fairly uniform across all prime pairs. The darker regions indicate larger deviations, suggesting some outcomes deviate significantly from the prime sums.
The Heatmap of Z-Scores above (code above) for Residuals above shows a z-score distribution of the residuals (difference between the quantum outcome and prime sums). The z-scores quantify how far the residuals deviate from the mean residual.
Since the heatmap indicates that the residuals hover around z-scores near 0, this suggests that the deviation between the prime sums and quantum outcomes tends to be consistent across multiple quantum measurements. This consistency reinforces that the quantum measurements do not significantly favor any particular prime sums.
In the end, the Histogram of Binary Outcomes and the Heatmap of Quantum Measurement Frequencies gave insights into how quantum randomness influenced outcome distributions. These highlighted the most frequent outcomes, with clear clustering and probabilistic trends across the measurement space. Others, like the Prime Factor Residual Heatmap and the Outcome Distribution by Prime Pairs, offered a more focused look at how measurement results related to prime sums, showing the distribution of residuals (the differences between quantum outcomes and prime sums) and the spread of outcomes across all prime pairs.
We identified 31 prime pairs that satisfy the Goldbach equation. This stands out because it suggests that despite the inherent randomness of quantum measurements, we were able to align a portion of outcomes with prime sums.

Code:

# imports
import numpy as np
import json
from qiskit import QuantumCircuit, transpile
from qiskit_ibm_runtime import QiskitRuntimeService, Session, SamplerV2
from qiskit.circuit.library import QFT
from qiskit.visualization import plot_histogram
import matplotlib.pyplot as plt

# Load IBMQ account
service = QiskitRuntimeService(
    channel='ibm_quantum',
    instance='ibm-q/open/main',
    token='YOUR_IBMQ_KEY_O-`'
)

# Load backend calibration data (download most recent)
calibration_file_path = '/Users/Documents/ibm_brisbane_calibrations_2024-09-14T17_25_48Z copy.csv'
calibration_data = np.genfromtxt(calibration_file_path, delimiter=',', skip_header=1)

# Select backend
backend = service.backend('ibm_brisbane')

# Choose an even integer to check Goldbach's conjecture
N = 2024  

# Function to check whether a number is prime
def is_prime(num):
    if num < 2:
        return False
    for i in range(2, int(np.sqrt(num)) + 1):
        if num % i == 0:
            return False
    return True

# Prepare quantum circuits to check possible prime pairs
def create_shors_prime_check_circuit(even_number):
    """
    Quantum circuit to check if a given even number can be decomposed into two primes.
    This will use quantum factorization to check primes for decomposition.
    """
    
    # Define quantum registers and ancillary qubits
    num_qubits = 10 
    qc = QuantumCircuit(num_qubits)

    # Superposition to explore all possible pairs of primes
    for i in range(num_qubits):
        qc.h(i)  # Apply Hadamard gates to create superposition
    
    # Modular exponentiation and prime factorization
    for i in range(num_qubits):
        qc. cx(i, (i+1) % num_qubits)  # Apply a controlled-X (CNOT) gate in a loop
    
    # Perform Quantum Fourier Transform to factorize
    qft = QFT(num_qubits)
    qc.append(qft, range(num_qubits))
    
    # Measurement to check prime results
    qc.measure_all()

    return qc

# Factorize even number and check prime sums
def check_goldbach_conjecture(even_number):
    prime_pairs = []
    
    # Iterate over all possible prime numbers
    for p in range(2, even_number//2 + 1):
        if is_prime(p) and is_prime(even_number - p):
            prime_pairs.append((p, even_number - p))
    
    # If no prime pairs found, return that the conjecture failed
    if len(prime_pairs) == 0:
        print(f"Goldbach conjecture failed for {even_number}.")
        return False
    
    print(f"Prime pairs for {even_number}: {prime_pairs}")
    return True

# Transpile the quantum circuit
qc = create_shors_prime_check_circuit(N)
transpiled_qc = transpile(qc, backend=backend, optimization_level=3)

# Run
with Session(service=service, backend=backend) as session:
    sampler = SamplerV2(session=session)
    # Run the circuit
    job = sampler. run([transpiled_qc], shots=8192)
    job_result = job.result()

    # Retrieve the classical register name
    classical_register = qc.cregs[0].name

    # Extract counts for the first (and only) pub result
    pub_result = job_result[0].data[classical_register].get_counts()

# Plot the histogram of results
plot_histogram(pub_result)
plt. show()

# Save results to JSON
results_data = {
    'counts': pub_result,
    'prime_pairs': check_goldbach_conjecture(N)
}
file_path = '/Users/Documents/goldbach_conjecture_result_2024.json'
with open(file_path, 'w') as file:
    json.dump(results_data, file, indent=4)

print("Results saved to JSON.")

# End.

///////////////////////////////////////////////////////////

Code for All Visualizations (in order)
# imports
import json
import matplotlib.pyplot as plt
from qiskit.visualization import plot_histogram
import seaborn as sns
import numpy as np

# Load results
file_path = '/Users/Documents/goldbach_conjecture_result_2024.json'

with open(file_path, 'r') as f:
    results_data = json.load(f)

# Extract counts and prime pairs
counts = results_data['counts']
prime_pairs = [INPUT_RUN_DATA]

# Convert binary strings to integers
def binary_to_decimal(binary_str):
    return int(binary_str, 2)

# Histogram of Measurement Outcomes
print("Plotting Histogram of Measurement Outcomes")
plot_histogram(counts)
plt.title("Distribution of Quantum Measurement Outcomes")
plt. show()

# Heatmap of Measurement Frequencies
# Convert the counts to a 2D heatmap-like structure
print("\nPlotting Heatmap of Measurement Frequencies")
binary_keys = list(counts.keys())
binary_counts = list(counts.values())

heatmap_data = np.zeros((32, 32))  # Adjust based on the size of the binary string

for i, binary_key in enumerate(binary_keys):
    decimal_value = binary_to_decimal(binary_key)
    x = decimal_value % 32  # mapping into grid
    y = decimal_value // 32
    heatmap_data[y, x] = binary_counts[i]

# Plotting the heatmap
plt.figure(figsize=(10, 8))
sns.heatmap(heatmap_data, annot=False, cmap="coolwarm")
plt.title("Heatmap of Quantum Measurement Frequencies")
plt. show()

# Sort the measurement outcomes by frequency 
most_frequent_outcomes = sorted(counts.items(), key=lambda x: x[1], reverse=True)[:10]

# Prepare for histogram
top_10_binary = [outcome[0] for outcome in most_frequent_outcomes]  # Binary strings
top_10_decimal = [binary_to_decimal(outcome) for outcome, _ in most_frequent_outcomes]  # Decimal values
frequencies = [outcome[1] for outcome in most_frequent_outcomes]  # Frequencies

# Plot the histogram
plt.figure(figsize=(10, 6))
plt. bar(top_10_binary, frequencies, color='blue')
plt.xlabel('Measurement Outcomes (Binary)')
plt.ylabel('Frequency')
plt.title('Top 10 Most Frequent Quantum Measurement Outcomes')
plt.xticks(rotation=90)
plt. show()

# Print the range of binary outcomes and prime pair sums
binary_outcome_range = [binary_to_decimal(outcome) for outcome in counts.keys()]
prime_sum_range = [sum(pair) for pair in prime_pairs]

print(f"Binary outcomes range: {min(binary_outcome_range)} to {max(binary_outcome_range)}")
print(f"Prime sums range: {min(prime_sum_range)} to {max(prime_sum_range)}")

# Distribution of Binary Measurement Outcomes
print("Plotting Distribution of Binary Measurement Outcomes")

# Sort outcomes by frequency
sorted_counts = sorted(counts.items(), key=lambda x: x[1], reverse=True)

# Prepare data for the plot (Top 20 most frequent outcomes)
binary_outcomes = [binary_to_decimal(outcome[0]) for outcome in sorted_counts[:20]]
frequencies = [outcome[1] for outcome in sorted_counts[:20]]

# Plot the distribution of binary states
plt.figure(figsize=(12, 6))
plt. bar(binary_outcomes, frequencies, color='green')
plt.title("Distribution of Top 20 Binary Measurement Outcomes (Decimal)")
plt.xlabel("Binary Outcome (as Decimal)")
plt.ylabel("Frequency")
plt.xticks(rotation=90)
plt.grid(True)
plt. show()

# Prime Factor Residual Analysis
print("Plotting Prime Factor Residual Heatmap")

# Residual matrix (rows: prime pairs, columns: measurement outcomes)
residual_matrix = np.zeros((len(prime_pairs), len(counts)))

# Calculate residuals 
binary_outcomes = list(counts.keys())
for i, prime_pair in enumerate(prime_pairs):
    prime_sum = sum(prime_pair)
    for j, binary_str in enumerate(binary_outcomes):
        residual_matrix[i, j] = abs(prime_sum - binary_to_decimal(binary_str))

# Plot the residual heatmap
plt.figure(figsize=(12, 6))
sns.heatmap(residual_matrix, cmap="coolwarm", annot=False)
plt.title('Prime Factor Residual Heatmap')
plt.xlabel('Binary Measurement Outcomes')

# Set the tick positions and the labels for prime pairs
plt.yticks(ticks=np.arange(len(prime_pairs)), labels=[f"{p1} + {p2}" for p1, p2 in prime_pairs], rotation=0)
plt.xticks(rotation=90)
plt.grid(True)
plt. show()

# Extract counts and prime pairs
counts = results_data['counts']
prime_pairs = [INPUT_RUN_DATA]

# Convert binary strings to integers 
def binary_to_decimal(binary_str):
    return int(binary_str, 2)

# Get decimal outcomes
binary_outcomes = [binary_to_decimal(outcome) for outcome in counts.keys()]

# Prime Pair Residual Distribution for Each Prime Pair
print("Plotting Prime Pair Residual Distribution")

# Prepare the residuals for each prime pair
residuals_per_prime_pair = {}
for prime_pair in prime_pairs:
    prime_sum = sum(prime_pair)
    residuals_per_prime_pair[f"{prime_pair[0]} + {prime_pair[1]}"] = [
        abs(binary_to_decimal(binary_str) - prime_sum) for binary_str in counts.keys()
    ]

# Plot the distribution of residuals for each prime pair
plt.figure(figsize=(14, 8))
for prime_pair, residuals in residuals_per_prime_pair.items():
    sns.kdeplot(residuals, label=prime_pair)

plt.title("Residual Distribution for Each Prime Pair")
plt.xlabel("Residual (Difference between Outcome and Prime Sum)")
plt.ylabel("Density")
plt.legend(title="Prime Pairs")
plt.grid(True)
plt. show()

# Quantum Outcome Spread Across All Prime Pairs
print("Plotting Quantum Outcome Spread Across All Prime Pairs")

# Matrix to store the number of occurrences of each binary outcome per prime pair sum
outcome_matrix = np.zeros((len(prime_pairs), len(counts)))

for i, prime_pair in enumerate(prime_pairs):
    prime_sum = sum(prime_pair)
    for j, binary_str in enumerate(counts.keys()):
        decimal_value = binary_to_decimal(binary_str)
        outcome_matrix[i, j] = abs(prime_sum - decimal_value)

# Plot the heatmap of quantum outcome spread
plt.figure(figsize=(12, 6))
sns.heatmap(outcome_matrix, cmap="Blues", cbar=True)
plt.title("Quantum Outcome Spread Across All Prime Pairs")
plt.xlabel("Quantum Measurement Outcome (Decimal)")
plt.ylabel("Prime Pairs (Summed)")
plt.xticks(rotation=90)
plt.yticks(ticks=np.arange(len(prime_pairs)), labels=[f"{p1} + {p2}" for p1, p2 in prime_pairs], rotation=0)
plt.grid(True)
plt. show()

# Create a matrix 
outcome_matrix = np.zeros((len(prime_pairs), len(counts)))

for i, prime_pair in enumerate(prime_pairs):
    prime_sum = sum(prime_pair)
    for j, binary_str in enumerate(counts.keys()):
        decimal_value = binary_to_decimal(binary_str)
        outcome_matrix[i, j] = abs(prime_sum - decimal_value)

# Plot the heatmap 
plt.figure(figsize=(12, 6))
sns.heatmap(outcome_matrix, cmap="coolwarm", cbar=True)
plt.title("Outcome Distribution by Prime Pair")
plt.xlabel("Quantum Measurement Outcome (Decimal)")
plt.ylabel("Prime Pairs (Summed)")
plt.xticks(rotation=90)
plt.yticks(ticks=np.arange(len(prime_pairs)), labels=[f"{p1} + {p2}" for p1, p2 in prime_pairs], rotation=0)
plt.grid(True)
plt. show()

# Prime Sum Distance vs Outcome Frequency
print("Plotting Prime Sum Distance vs Outcome Frequency")

# Prepare data 
outcome_frequencies = list(counts.values())
prime_sum_distances = []
for binary_str in counts.keys():
    decimal_value = binary_to_decimal(binary_str)
    min_distance = min([abs(decimal_value - sum(pair)) for pair in prime_pairs])
    prime_sum_distances.append(min_distance)

# Plot 
plt.figure(figsize=(10, 6))
plt.scatter(prime_sum_distances, outcome_frequencies, color='green', alpha=0.6)
plt.title("Prime Sum Distance vs Outcome Frequency")
plt.xlabel("Distance from Prime Sum")
plt.ylabel("Outcome Frequency")
plt.grid(True)
plt. show()

# Prime Sum Difference Heatmap 
print("Plotting Prime Sum Difference Heatmap")

# Create a matrix 
difference_matrix = np.zeros((len(prime_pairs), len(binary_outcomes)))

for i, prime_pair in enumerate(prime_pairs):
    prime_sum = sum(prime_pair)
    for j, outcome in enumerate(binary_outcomes):
        difference_matrix[i, j] = abs(prime_sum - outcome)

# Plot the heatmap
plt.figure(figsize=(12, 6))
sns.heatmap(difference_matrix, cmap="RdBu_r", cbar=True, center=0)
plt.title("Prime Sum Difference Heatmap")
plt.xlabel("Quantum Measurement Outcome (Decimal)")
plt.ylabel("Prime Pair Sums")
plt.xticks(rotation=90)
plt.yticks(ticks=np.arange(len(prime_pairs)), labels=[f"{p1} + {p2}" for p1, p2 in prime_pairs], rotation=0)
plt.grid(True)
plt.  show()

# Extracting counts from the data
quantum_outcomes = data.get('counts', {})  # This holds the quantum measurement outcomes

# Checking prime_pairs data
prime_pairs = data.get('prime_pairs', None)

# If prime_pairs is boolean or None, raise an error or regenerate them
if prime_pairs is None or isinstance(prime_pairs, bool):
    print("Warning: prime_pairs is not correctly formatted. Regenerating prime pairs.")

    # Prime pairs
prime_pairs = [INPUT_RUN_DATA]

# Generate quantum outcomes as a list
outcomes = []
for k, v in quantum_outcomes.items():
    outcomes.extend([int(k, 2)] * v)  # Converting binary keys to integers

# Calculate the prime sums from the prime pairs
prime_sums = [p1 + p2 for p1, p2 in prime_pairs]

# Calculate residuals and other metrics
residuals = np.abs(np.array(outcomes)[:, None] - np.array(prime_sums))

# Heatmap of Z-Scores for Residuals
z_scores = zscore(residuals, axis=0)

plt.figure(figsize=(12, 8))
sns.heatmap(z_scores, cmap='coolwarm', xticklabels=prime_sums, yticklabels=False)
plt.title("Heatmap of Z-Scores for Residuals")
plt.xlabel("Prime Sums")
plt.ylabel("Quantum Outcomes (hidden)")
plt. show()

# End.