A Quantum Neural Network on IBM's 127-Qubit Quantum Computer Kyoto
This Qiskit experiment is designed to explore Quantum Neural Networks (QNNs) for pattern recognition, specifically focusing on classifying data points based on their angular position in a 2-dimensional space. It uses IBM's 127-Qubit Kyoto to perform tasks that involve quantum state preparation, parameterized quantum circuit (PQC) execution, and optimization of parameters based on the outcome of measurements. The QNN's parameters are optimized using a classical optimization algorithm (COBYLA) to minimize a loss function that reflects the accuracy of the network's predictions. This is done in two circuits, first running the experiment, and second analyzing the results post-run.
Code Walkthrough
1. Data Generation:
Points (x,y) on a unit circle are generated with angles uniformly distributed between 0 and 2π.
Each point is labeled based on its angle, θ, such that points in specific angular ranges (0 < θ < π/2 or π < θ < (3π)/2) are assigned one label, and points outside these ranges are assigned another.
This results in a dataset {(x_i, y_i)}^N i = 1 where x_i represents the 2D coordinates of the i-th point, and y_i is its label.
2. Data Encoding into Quantum States:
A quantum circuit is constructed to map a data point (x, y) onto the state of a qubit.
The mapping is achieved through the use of quantum gates (universal U gate) that transform the initial state of the qubit based on the coordinates of the point.
The transformation applied by the U gate is parameterized by angles that are functions of the point's coordinates, encoding the classical data into a quantum state. Given a data point (x, y), the encoding process transforms it into a quantum state ∣ψ⟩ using a quantum circuit that applies gates parameterized by the data point's coordinates.
3. Quantum Neural Network (QNN) Design:
The QNN is designed as a parameterized quantum circuit (PQC) with tunable gates that allow for the learning process.
The circuit consists of rotation gates (R_x, R_y) and controlled-NOT (CNOT) gates for entanglement, with parameters θ representing the weights of the neural network.
4. Loss Calculation and Objective Function:
The loss function quantifies the difference between the predicted and actual labels of the data points.
After executing the QNN with a given set of parameters, the output quantum state is measured. The measurement outcomes are used to estimate the probability of observing a state corresponding to the correct label.
The loss for a single data point is calculated using the cross-entropy between the observed probabilities and the true label, facilitating gradient-based optimization.
The loss for a data point is calculated as:
where p is the probability of measuring the qubit in the state corresponding to the correct label y.
5. Optimization Process:
The parameters of the QNN are optimized using the COBYLA optimization algorithm, a classical optimization good for problems with noisy gradients, as encountered in quantum systems.
The optimization aims to minimize the loss function across the dataset, adjusting the parameters of the QNN to improve its prediction accuracy.
The experiment involves 230 computed jobs with 256 shots each with. The objective function to be minimized is the average loss over all data points in the batch or dataset, with COBYLA used to find the set of parameters θ that minimizes this average loss.
6. Training and Validation:
The dataset is split into training and validation subsets to evaluate the performance of the QNN and avoid overfitting.
The QNN is trained on the training subset, and its performance is periodically evaluated on the validation set to monitor progress and generalize ability.
7. Results Serialization:
After training, the optimized parameters of the QNN, along with training and validation losses are serialized into a JSON.
Quantum states of the system at different points in training are recorded to study the evolution of the QNN's representations.
1. Loading Calibration Data:
Calibration data from the runs on Kyoto are loaded.
2. Quantum Neural Network (QNN) Initialization:
A Quantum Circuit is generated. Each qubit's state can be manipulated using rotation gates (rx gates), which are parameterized by θ, representing the weights of the neural network.
3. Fidelity Calculation:
Fidelity between two quantum states is calculated using the formula:
where p_0 and p_1 are the predicted probabilities, and q_0 and q_1 are the expected probabilities of the quantum state being in 0 or 1. Fidelity measures the closeness of two quantum states.
4. Custom Hybrid Loss Function:
A custom hybrid loss function is defined, combining cross-entropy loss and fidelity. The cross-entropy:
calculates the difference between the predicted probabilities and actual labels. The fidelity adjusts the loss based on the similarity between the predicted and expected quantum states. A regularization parameter (lambda_reg) balances the contribution of fidelity to the total loss. Loss Calculation Using Measurement Outcomes:
For each measurement, the loss is computed based on the cross-entropy between the observed probabilities (obtained from the runs) and the true labels. Probabilities are adjusted using an epsilon to avoid undefined logarithms.
Optimization Process:
The QNN parameters are optimized using a classical optimization technique (COBYLA) to minimize the loss function. The process iteratively updates the QNN parameters (θ) and evaluates the loss, aiming to find the set that leads to the lowest loss.
Visualization and Analysis:
The loss values for each optimization iteration are visualized using an initial bar chart. The history of optimization, including parameters and loss values, is saved into a json.
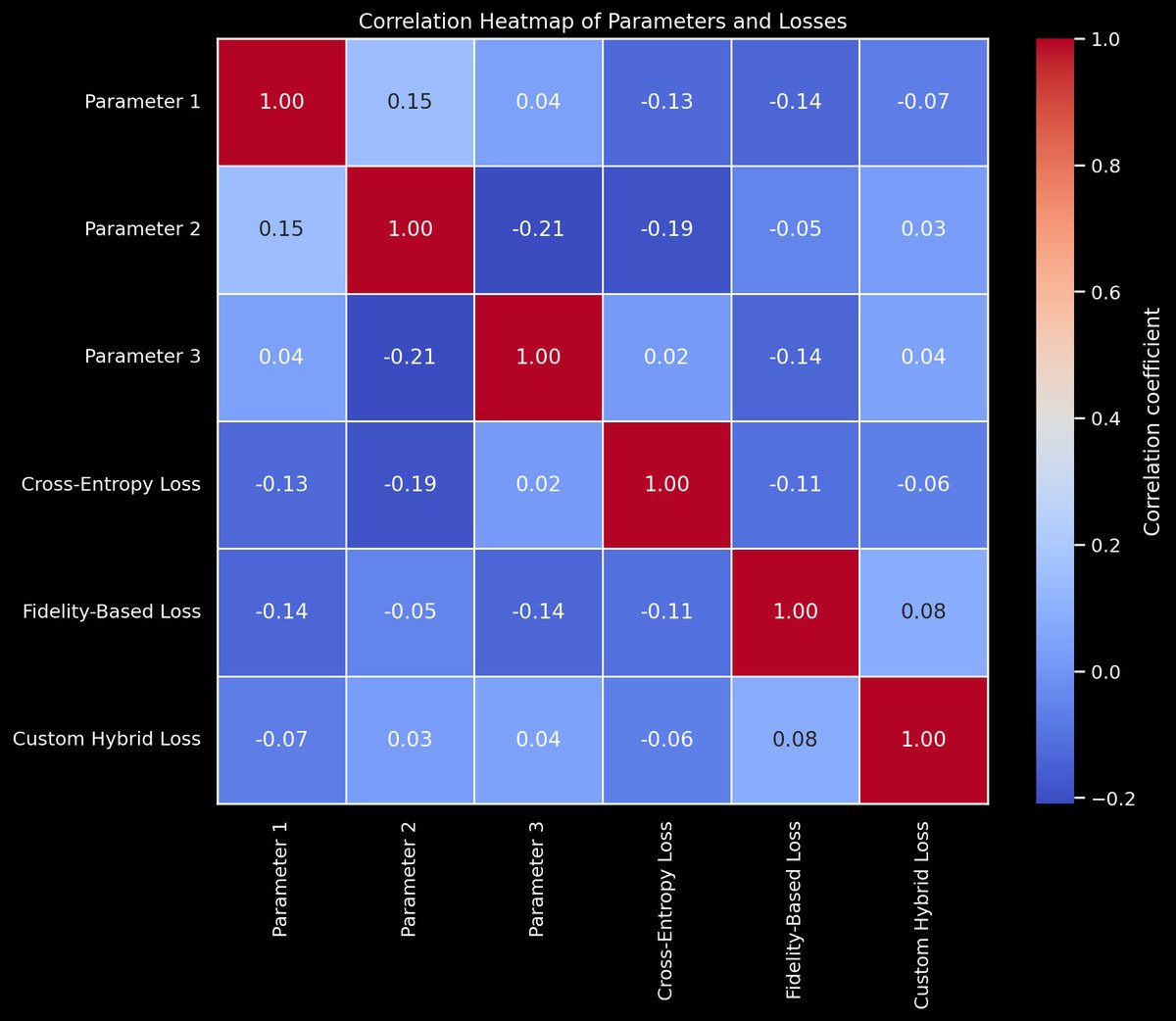
Optimization Loss Values for Each Loss Function:
Cross-Entropy Loss: 1.2966822024302034
Fidelity-Based Loss: 1.298556642044095
Custom Hybrid Loss: 0.0037488792277833305
Insight:
The Custom Hybrid Loss function did significantly better than the other two. It incorporates both the predictive accuracy and the quantum state fidelity into a single metric. By doing so, it can guide the optimization process more effectively than if these aspects were considered separately. This novel approach ensures that the optimization does not overly favor one aspect at the expense of the other, potentially leading to a more optimal set of parameters that achieve lower overall loss. This is a promising result.
In the end, we have completed and analyzed a basic Quantum Neural Network on IBM Osaka. Quantum systems are inherently noisy environments but it's amazing that we can begin to optimize these kinds of networks on qubits. Just the beginning of this kind of exploration.
Code:
Backend Circuit:
import numpy as np
import pandas as pd
from qiskit import Aer, QuantumCircuit, execute, IBMQ
from qiskit.circuit import ParameterVector
from qiskit.quantum_info import Statevector
import json
from scipy.optimize import minimize
from qiskit_algorithms.optimizers import COBYLA
# IBM quantum account
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibm_kyoto') # Adjust this to your specific backend
print("Using backend: ", backend)
# Load calibration data
calibration_data_path = '/Users/Documents/ibm_kyoto_calibrations_2024-03-07T20_24_57Z.csv' # Calibration file
calibration_data = pd. read_csv(calibration_data_path, header=1)
# Data Generation and Preparation
def generate_data(num_samples=50): # Keep the dataset size reasonable for the scope of training
angles = np.random.uniform(low=0, high=2*np.pi, size=num_samples)
data = np.array([np.cos(angles), np.sin(angles)]).T
labels = np.where(np.logical_or(np.logical_and(angles > 0, angles < np.pi/2),
np.logical_and(angles > np.pi, angles < 3*np.pi/2)), 1, 0)
return data, labels
def encode_data_into_qubit(data_point):
x, y = data_point
theta_qubit = np.arctan2(y, x)
r_qubit = np.sqrt(x**2 + y**2)
qc = QuantumCircuit(1)
qc.u(theta_qubit, r_qubit, 0, 0)
return qc
# QNN
def create_efficient_qnn(qubits):
qc = QuantumCircuit(qubits)
parameters = ParameterVector('θ', length=3*qubits)
index = 0
for q in range(qubits):
qc.rx(parameters[index], q)
index += 1
for q in range(qubits):
qc.ry(parameters[index], q)
index += 1
if qubits > 1:
for q in range(qubits - 1):
qc.cnot(q, q + 1)
return qc
def calculate_loss(probabilities, label):
prob_of_1 = probabilities.get('1', 0) / 1024
loss = -((label * np.log(prob_of_1 + 1e-10)) + ((1 - label) * np.log(1 - prob_of_1 + 1e-10)))
return loss
def objective_function(params, data, label, qnn, backend):
param_dict = {param: val for param, val in zip(qnn.parameters, params)}
data_circuit = encode_data_into_qubit(data)
combined_circuit = data_circuit.compose(qnn.assign_parameters(param_dict))
combined_circuit.measure_all()
job = execute(combined_circuit, backend, shots=256)
result = job.result().get_counts(combined_circuit)
probabilities = {state: counts for state, counts in result.items()}
loss = calculate_loss(probabilities, label)
return loss
def batch_train_qnn(data, labels, qnn, backend, iterations=2, batch_size=10): # Adjusted to ensure 40 total runs
optimizer = COBYLA(maxiter=1) # Limit the optimizer iterations to manage execution time
training_losses = []
validation_losses = []
quantum_states = []
# Split data into training (80%) and validation (20%) sets
split_idx = int(0.8 * len(data))
training_data, validation_data = data[:split_idx], data[split_idx:]
training_labels, validation_labels = labels[:split_idx], labels[split_idx:]
params = np.random.rand(len(qnn.parameters)) * 2 * np.pi # Initial parameter values
for it in range(iterations):
shuffled_indices = np.random.permutation(len(training_data))
training_data, training_labels = training_data[shuffled_indices], training_labels[shuffled_indices]
for start_idx in range(0, len(training_data), batch_size):
end_idx = min(start_idx + batch_size, len(training_data))
batch_data = training_data[start_idx:end_idx]
batch_labels = training_labels[start_idx:end_idx]
for data_point, label in zip(batch_data, batch_labels):
result = minimize(lambda p: objective_function(p, data_point, label, qnn, backend),
params, method='COBYLA')
params = result.x # Update parameters based on optimization
train_loss = np.mean([objective_function(params, dp, lbl, qnn, backend) for dp,
lbl in zip(training_data, training_labels)])
training_losses.append(train_loss)
val_loss = np.mean([objective_function(params, dp, lbl, qnn, backend) for dp,
lbl in zip(validation_data, validation_labels)])
validation_losses.append(val_loss)
# Record quantum state of first training data point
if backend. name == 'statevector_simulator' and it % 2 == 0:
sv = execute(encode_data_into_qubit(training_data[0]).compose(qnn.assign_parameters(params)),
Aer.get_backend('statevector_simulator')).result().get_statevector()
quantum_states.append(sv.tolist())
return params, training_losses, validation_losses, quantum_states
# Training and analysis
data, labels = generate_data(50) # Generate a smaller dataset for this training session
qnn = create_efficient_qnn(1) # Using a single qubit for this example
optimized_params, training_losses, validation_losses, quantum_states =
batch_train_qnn(data, labels, qnn, backend, iterations=2, batch_size=10) # Adapted for 40 total runs
# serialization of results for complex numbers
def complex_encoder(z):
if isinstance(z, complex):
return {"real": z.real, "imag": z.imag}
else:
raise TypeError(f"Object of type '{z.__class__.__name__}' is not JSON serializable")
output_data = {
'optimized_params': optimized_params.tolist(),
'final_loss': training_losses[-1],
'training_losses': training_losses,
'validation_losses': validation_losses,
'quantum_states': quantum_states
}
json_path = '/Users/O-'/QNN_HW_Run.json' # Adjust this to your desired output path
with open(json_path, 'w') as f:
json.dump(output_data, f, indent=4, default=complex_encoder)
print("Results saved to:", json_path)
Analysis Circuit:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from qiskit import Aer, execute, QuantumCircuit
from qiskit.circuit import ParameterVector
import json
# load calibration data
calibration_data_path = '/Users/Documents/ibm_kyoto_calibrations_2024-03-07T20_24_57Z.csv'
calibration_data = pd. read_csv(calibration_data_path)
# generate QNN
def create_qnn(num_qubits, num_parameters):
qc = QuantumCircuit(num_qubits)
parameters = ParameterVector('θ', num_parameters)
for i in range(num_qubits):
qc.rx(parameters[i], i) # Example usage of parameters
return qc, parameters
# Fidelity calculation
def calculate_fidelity(p_0, p_1, q_0, q_1):
return np.sqrt(p_0 * q_0) + np.sqrt(p_1 * q_1)
# custom hybrid loss function
def custom_hybrid_loss(y_true, p_pred, q_0, q_1, lambda_reg=0.5):
p_0 = 1 - p_pred
p_1 = p_pred
fidelity = calculate_fidelity(p_0, p_1, q_0, q_1)
cross_entropy_loss = -np.mean(y_true * np.log(p_pred) + (1 - y_true) * np.log(1 - p_pred))
return cross_entropy_loss + lambda_reg * (1 - fidelity)
# Calculate_loss function
def calculate_loss_from_measurements(measurement_outcomes, true_labels):
epsilon = 1e-10 # Small number to avoid log(0)
total_shots = sum(measurement_outcomes.values())
p0 = measurement_outcomes.get('0x0', 0) / total_shots
p1 = measurement_outcomes.get('0x1', 0) / total_shots
p0 = np.clip(p0, epsilon, 1-epsilon) # Ensure p0 is between 0 and 1
p1 = np.clip(p1, epsilon, 1-epsilon) # Ensure p1 is between 0 and 1
# probability
p = p1 if true_labels == 1 else p0
# Computing cross-entropy loss
if true_labels == 1:
loss = -np.log(p)
else:
loss = -np.log(1 - p)
return loss
# Run optimization and collect history
def run_optimization(initial_params, measurement_results):
optimization_history = {'parameters': [], 'loss': []}
# Extract probabilities from measurement results
total_counts = sum(measurement_results.values())
p_0 = measurement_results['0x0'] / total_counts
p_1 = measurement_results['0x1'] / total_counts
q_0, q_1 = 0.8, 0.2
# single data point
true_labels = np.array([1])
p_pred = p_1
# Calculate each loss
fidelity_loss = 1 - calculate_fidelity(p_0, p_1, q_0, q_1)
hybrid_loss = custom_hybrid_loss(true_labels, p_pred, q_0, q_1, lambda_reg=0.5)
cross_entropy_loss = calculate_loss_from_measurements({'0x0': p_0, '0x1': p_1}, true_labels)
optimization_history['loss'].append({
'Cross-Entropy Loss': cross_entropy_loss,
'Custom Hybrid Loss': hybrid_loss,
'Fidelity-Based Loss': fidelity_loss,
})
def objective_function(params):
return hybrid_loss
result = minimize(objective_function, initial_params, method='COBYLA', options={'maxiter': 100})
optimization_history['parameters'].append(initial_params.tolist())
return optimization_history, result
# analysis script
if __name__ == "__main__":
num_qubits = 1
num_parameters = 3
measurement_results = {"0x0": 186, "0x1": 70}
initial_params = np.random.rand(num_parameters) * 2 * np.pi
optimization_history, result = run_optimization(initial_params, measurement_results)
# loss results for each loss function
print("Optimization Loss Values for Each Loss Function:")
for loss_name, loss_value in optimization_history['loss'][0].items():
print(f"{loss_name}: {loss_value}")
# dark background for plots
plt. style.use('dark_background')
# bar chart for loss values
plt.figure(figsize=(10, 5))
loss_values = optimization_history['loss'][0]
bars = plt. bar(loss_values.keys(), loss_values.values(), color='white', edgecolor='white')
# text
for bar in bars:
yval = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2, yval, round(yval, 4), ha='center', va='bottom', color='white')
plt.title('Loss Values', color='white')
plt.xlabel('Loss Function', color='white')
plt.ylabel('Loss Value', color='white')
plt.tick_params(axis='x', colors='white')
plt.tick_params(axis='y', colors='white')
plt. show()
# Save json
save_path = '/Users/O-'/QNN_ANALYSIS_RUN.json'
with open(save_path, 'w') as f:
json_data = {
'optimization_history': optimization_history,
'final_result': {
'final_parameters': result.x.tolist(),
'final_loss': result. fun
}
}
json.dump(json_data, f, indent=4)
# end