Using Quantum Cryptography to Create a Secure Bitcoin Key on IBM's 127-Qubit Quantum Computer Osaka
This experiment uses quantum computing to generate a secure cryptographic key, then we convert this quantum-generated key into a format compatible with Bitcoin's cryptographic system. This process utilizes the inherent randomness of quantum mechanics through superposition and measurement of qubits. The experiment is conducted on IBM's 127-qubit quantum computer Osaka, utilizing Qiskit. After generating a binary key from quantum measurements, the key undergoes post-processing to convert it into a hexadecimal format, and finally into a Wallet Import Format (WIF) key for potential use in Bitcoin transactions. This experiment shows how quantum computing can enhance cryptography, providing a true increase in randomness and thus entropy in a system.
Code Walkthrough
1. Quantum Circuit Configuration:
127 qubits are initialized in their default state, |0⟩.
A Hadamard gate (H) is applied to each qubit. The Hadamard gate transforms the qubit into a superposition state, expressed as:
This state implies that upon measurement, the qubit has an equal probability of being observed as |0⟩ or |1⟩, embodying quantum randomness.
2. Binary Key Generation:
Two runs of the quantum circuit are executed to generate two 127-bit strings. An additional "11" is appended to these strings to reach a 256-bit binary key, aligning with the standard length of a Bitcoin private key.
3. Binary to Hexadecimal Conversion:
The 256-bit binary key is converted to a hexadecimal format using the binary to hexadecimal conversion principle, where each group of four binary digits corresponds to a single hexadecimal digit. This conversion is essential for the subsequent processing steps and aligns with common cryptographic keys.
4. Hexadecimal Key to Wallet Import Format (WIF) Conversion:
The hexadecimal key is prefixed with '80', indicating a private key for the Bitcoin mainnet.
The extended key undergoes two rounds of SHA-256 hashing, a cryptographic hash function producing a 256-bit output. This step enhances the security of the key.
The first four bytes of the second SHA-256 hash serve as a checksum, ensuring the integrity of the key during transmission or storage.
The original extended key, now with the checksum appended, is encoded using Base58. Unlike Base64, Base58 encoding avoids similar-looking characters, reducing the risk of key misinterpretation. The result is the private key in WIF, which is more user-friendly and compatible with Bitcoin wallets.
Using backend: ibm_osaka Job Status: job has successfully run Job Status: job has successfully run Generated Quantum Key (Binary): 0001100011100010000010011111000110000100101100001111110110110001000111
1000001001110101011011000101011010010011101011101101000
11111111101001001101111000001101111101110111100010010101000
101010010011001001011010001001011110010001100001111110111100
110010110111
Generated Quantum Key (Hex): 18e209f184b0fdb11e09d5b15a4ebb47fd26f06fbbc4a8a9325a25e461fbccb7
Generated Bitcoin Key (WIF): 5J1FBbKoyTQZCjJqYYBsYRXWRBeuVrgzNogsRTC7Ft1rH2mZtwK
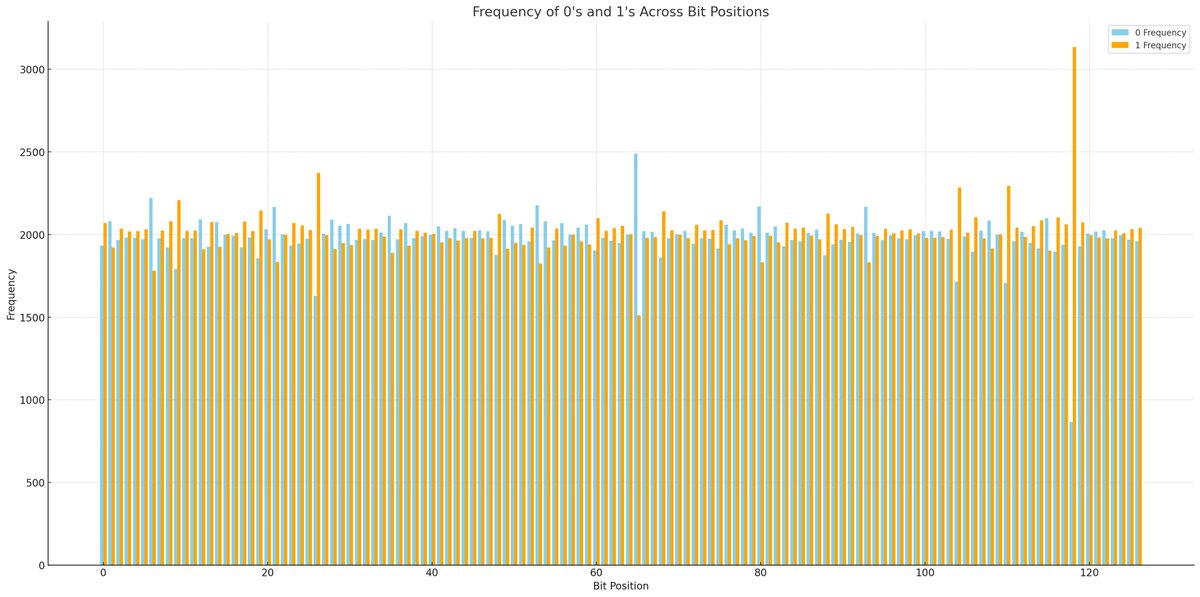
Symmetry and Imbalance: While some bit positions exhibit a near-symmetrical distribution between 0's and 1's, indicating unbiased quantum behavior, others show marked imbalances. This could be indicative of systematic errors, environmental noise affecting the qubits, or inherent biases in the quantum hardware.
Quantum Randomness: The spread of frequencies across bit positions illustrates the quantum randomness in generating each bit of the key. Ideally, in a perfectly balanced and noise-free system, we would expect to see a 50-50 distribution of 0's and 1's across all bit positions.
The ratio of '01' and '10' results to '00' results provides insight into the error rates during teleportation:
Specific Imbalances: Certain positions show significant deviation from the expected balance. For instance, position 26 shows a highly imbalanced ratio, favoring the outcome of 1's. This could be particularly interesting for further analysis to determine if specific qubits or positions consistently show such biases across multiple runs, which might indicate potential areas for hardware calibration or algorithmic adjustments.
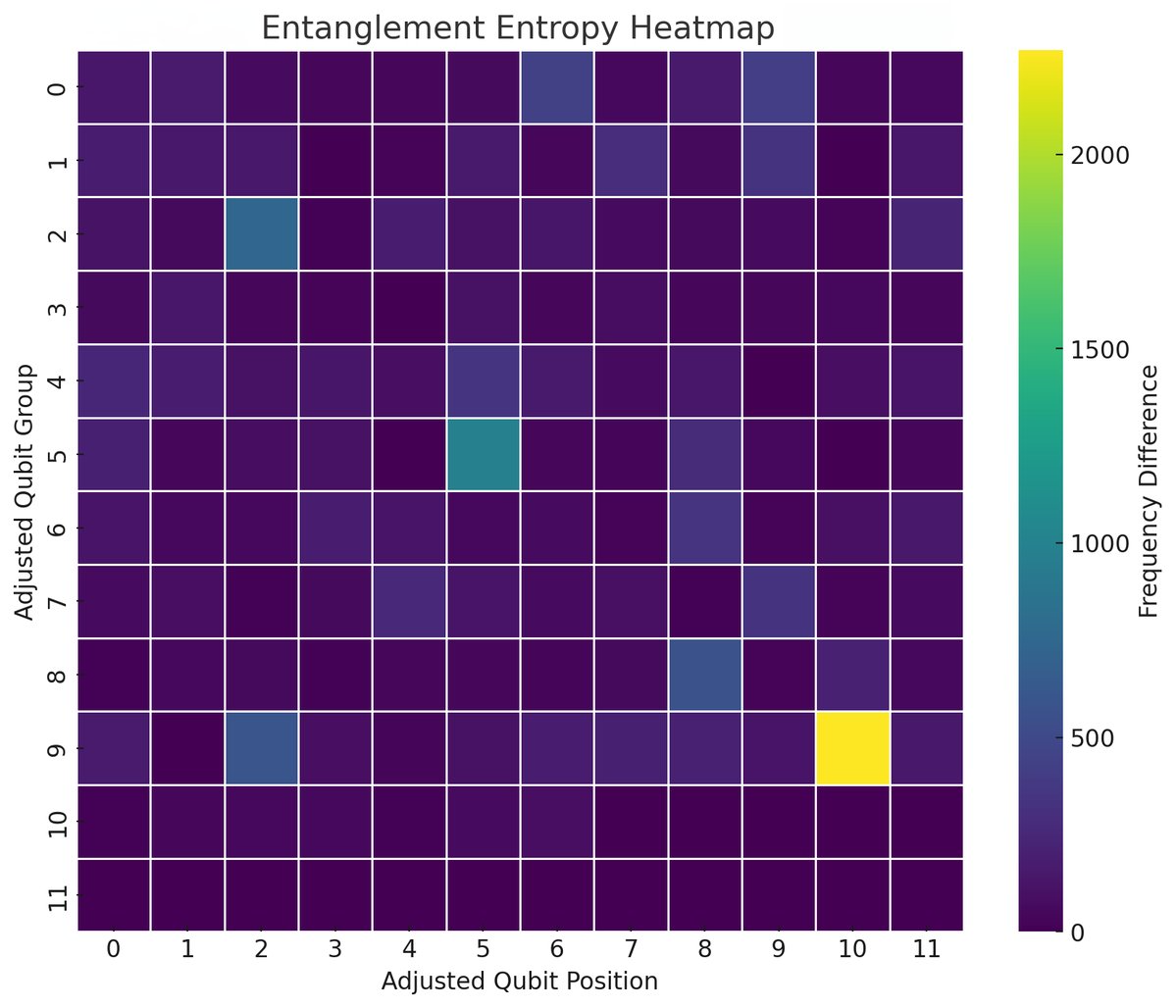
In the end, this experiment demonstrates a practical application of quantum computing's inherent randomness to generate a secure cryptographic key, and to thus increase entropy in cryptographic systems.
Code:
import json
import hashlib
import base58
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit, IBMQ, transpile, execute
from qiskit. tools.monitor import job_monitor
from qiskit.visualization import plot_histogram
# IBM Quantum account setup
IBMQ. save_account(‘YOUR_API_KEY_O-‘, overwrite=True) # Fill in your IBM Quantum token
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibm_osaka') # Update backend if necessary
print("Using backend: ", backend)
# Function to create and run a quantum circuit, generate a part of the secret key
def generate_key_part(num_qubits, backend):
# Create a quantum circuit with num_qubits
circ = QuantumCircuit(num_qubits)
# Apply Hadamard gate to each qubit to create superposition
for i in range(num_qubits):
circ.h(i)
# Measure all qubits
circ.measure_all()
# Compile and run the quantum circuit on the backend
compiled_circuit = transpile(circ, backend)
job = backend. run(compiled_circuit)
job_monitor(job) # Monitor the job's execution
# Retrieve the result
result = job.result()
counts = result.get_counts()
# Use the most frequent bitstring as part of the key
key_part = max(counts, key=counts.get)
return key_part
def sha256(data):
return hashlib.sha256(data).digest()
def hex_to_wif(hex_key):
# Add prefix (0x80 for mainnet)
extended_key = '80' + hex_key
# Double SHA-256 hash
first_hash = sha256(bytes.fromhex(extended_key))
second_hash = sha256(first_hash)
# Checksum is first 4 bytes of second hash
checksum = second_hash[:4]
# Append checksum
final_key = extended_key + checksum.hex()
# Base58 encode
wif_key = base58.b58encode(bytes.fromhex(final_key))
return wif_key.decode('utf-8')
# Generate the secret key parts using the quantum computer
key_part_1 = generate_key_part(127, backend)
key_part_2 = generate_key_part(127, backend)
# Concatenate 🐈⬛ the two parts and add any additional bits if needed to reach 256 bits
quantum_key_binary = key_part_1 + key_part_2 + "11" # Ensuring 256 bits
quantum_key_hex = hex(int(quantum_key_binary, 2))[2:].zfill(64)
# Convert the hex key to WIF
bitcoin_key = hex_to_wif(quantum_key_hex)
# Print the generated keys
print("Generated Quantum Key (Binary):", quantum_key_binary)
print("Generated Quantum Key (Hex):", quantum_key_hex)
print("Generated Bitcoin Key (WIF):", bitcoin_key)
# Save the keys to a json
with open('/Users/Documents/Q_BTC_Key.json', 'w') as f:
json.dump({
"Quantum Key (Binary)": quantum_key_binary,
"Quantum Key (Hex)": quantum_key_hex,
"Bitcoin Key (WIF)": bitcoin_key
}, f, indent=4)