Exploring Quantum Teleportation on IBM's 7-Qubit Quantum Computer Nairobi

Quantum teleportation is the transfer of quantum information (quantum states) from one particle to another over a distance, using quantum entanglement and classical communication. This experiment using qiskit demonstrates the principles of quantum teleportation on IBM's 7-Qubit Quantum Computer Nairobi. It illustrates the phenomena of superposition, entanglement, and the collapse of quantum states upon measurement.

Code Walkthrough
1. Initialization of the Quantum Circuit:
The circuit is initialized with 7 qubits. For teleportation, we focus on the first three qubits, with Qubits 0 and 1 being prepared in an entangled state and Qubit 2 as the target for teleportation.

2. Entanglement Creation between Qubits 0 and 1:

2. Hadamard Gate on Qubit 0:
The Hadamard gate creates a superposition state. It transforms the basis states as follows:

H∣0⟩ = ​(∣0⟩ + ∣1⟩)/sqrt(2)

H∣1⟩ = ​(∣0⟩ - ∣1⟩)/sqrt(2)

CNOT Gate between Qubit 0 and Qubit 1:
The Controlled-NOT gate entangles Qubit 0 with Qubit 1. Its operation can be described as:

CNOT∣x, y⟩ = ∣x, x ⊕ y⟩
where x, y are the states of the control and target qubits, and ⊕ represents the XOR operation.

3. Measurement and Collapse of Qubits 0 and 1:
The measurement of these qubits collapses their quantum state into one of the basis states. The state of each qubit becomes either ∣0⟩ or ∣1⟩, with probabilities dependent on their state prior to measurement.

4. Conditional Operation on Qubit 2:
Based on the measurement of Qubit 0, a conditional operation (Pauli-X gate) is applied to Qubit 2. The Pauli-X gate acts as a quantum bit-flip operation:

X∣0⟩ = ∣1⟩

X∣1⟩ = ∣0⟩
This step is crucial for the teleportation protocol as it completes the transfer of the quantum state from Qubit 0 to Qubit 2.

5. Execution of the Quantum Circuit:
The circuit is sent and executed on IBM's 7-Qubit Quantum Computer Nairobi.

6. Result Analysis:
The final states of the qubits are analyzed post-execution. The analysis involves interpreting the quantum state transfer fidelity, based on the observed probabilities of outcomes.

7. Data Saving and Extended Analysis:
The experimental results, along with the backend information, are saved for further analysis.

Results:

'0000000': 1900 occurrences

'0000001': 79 occurrences

'0000010': 111 occurrences

'0000011': 1910 occurrences

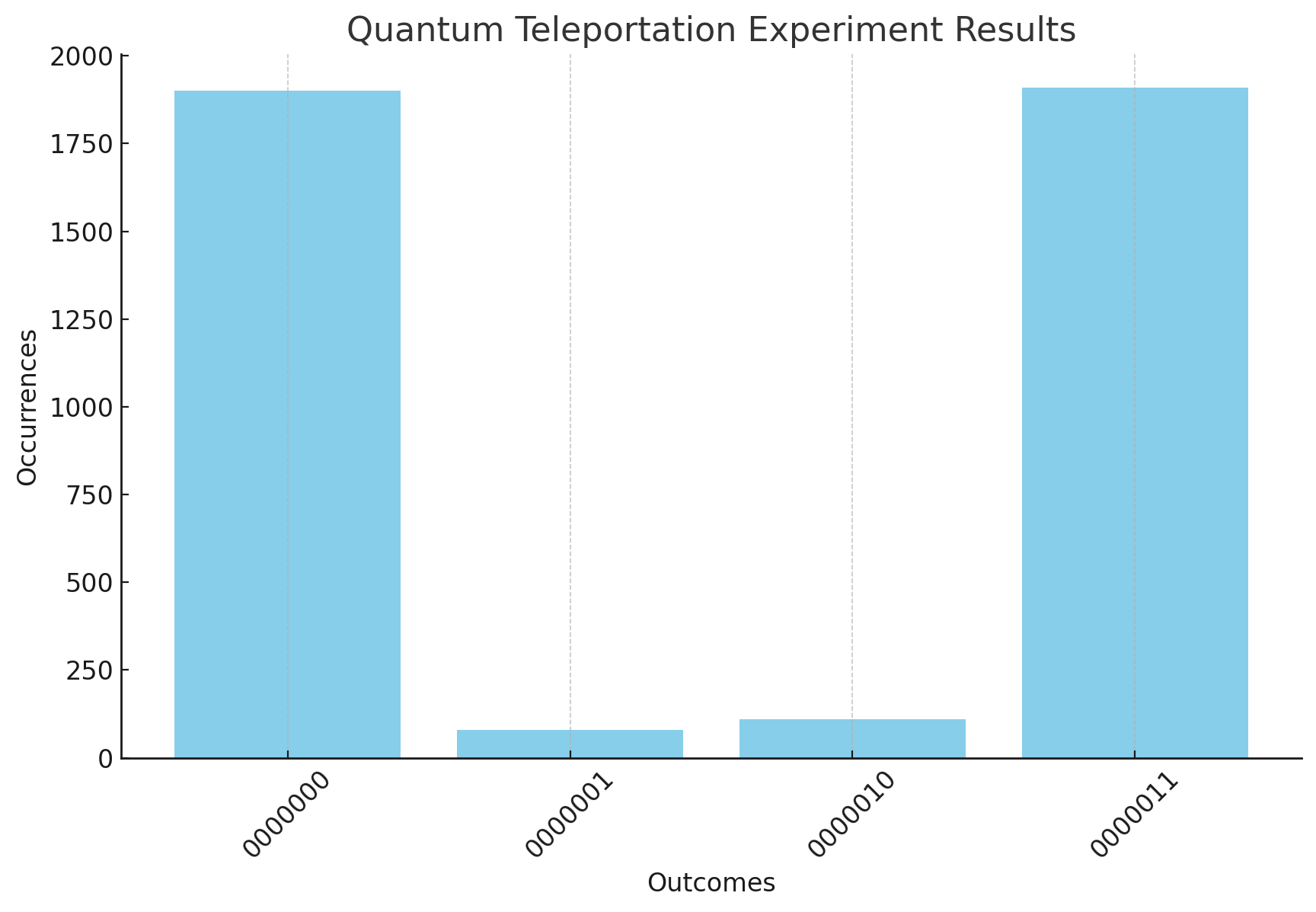
Dominant Outcomes:
The states '0000000' and '0000011' clearly dominate the results, with each having close to 1900 occurrences. This prominence suggests that the quantum teleportation protocol primarily resulted in these states, which is indicative of successful teleportation.

Success Indicators:
The high frequency of '0000000' and '0000011' compared to the other states suggests a high degree of fidelity in the teleportation process.

Error rate:
The small occurrence of the error states ('0000001' and '0000010') indicates small systematic errors or imperfections in the quantum circuit or the quantum computer itself, such as gate errors, decoherence, or measurement errors and is normal in real systems.

Above is a 3D Surface Plot for Probability Distributions providing a novel visualization of the quantum teleportation experiment's outcomes. The plot features a surface stretched over a mesh grid, where each axis (X and Y) represents indices of quantum states. The Z-axis displays the probability (normalized occurrences) of each state. The color variation across the surface represents different probability values, with the colormap providing a gradient from low to high probabilities.

Above is a heatmap of Normalized Quantum State Occurrences. The heatmap displays the normalized occurrences of each state in a color coded format. The warmer colors indicate higher occurrences, while cooler colors represent lower occurrences. This visualization provides an immediate sense of the distribution of outcomes across different quantum states, highlighting the most and least frequent outcomes.
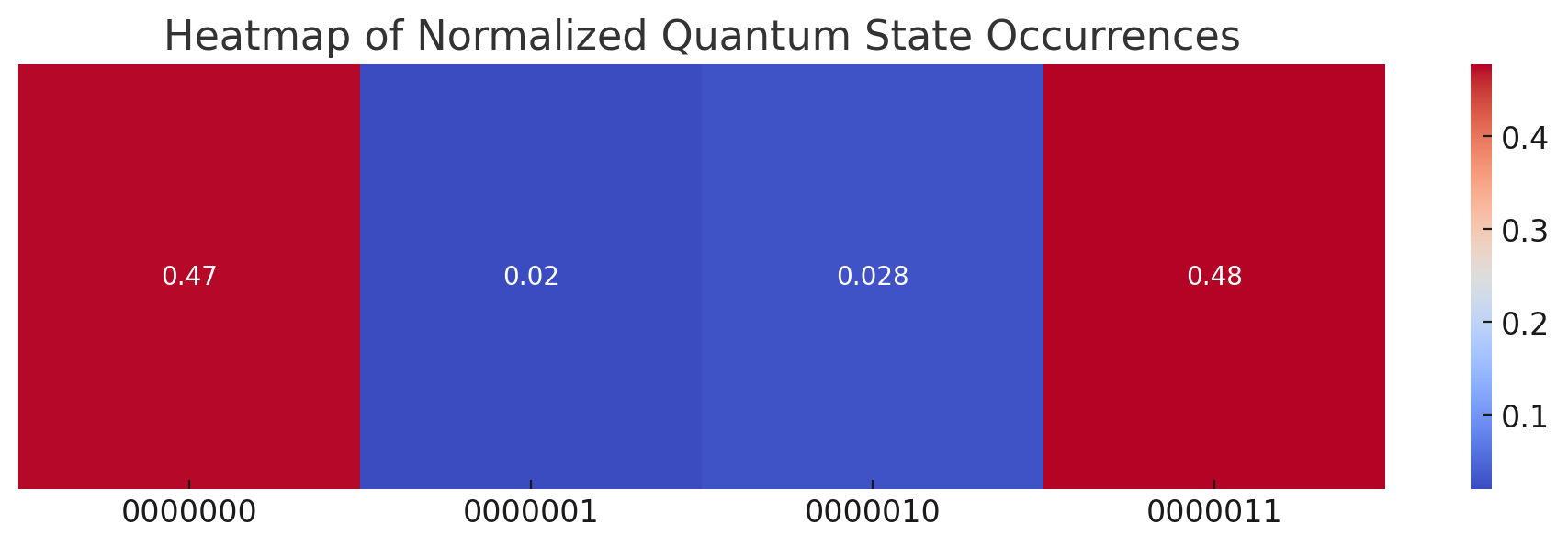
In the end, the experiment shows a strong indication of successful quantum teleportation, as evidenced by the dominant state outcomes. The experiment showcases quantum teleportation's unique ability to transfer quantum states using entanglement and measurement.

Code:

from qiskit import QuantumCircuit, transpile
from qiskit.visualization import plot_histogram
from qiskit. tools.monitor import job_monitor
from qiskit_ibm_provider import IBMProvider
import json
import matplotlib.pyplot as plt

# Insert your IBM API Key here
IBM_API_KEY = 'Your_Key_Here'

# Enable your IBMQ account using the new provider
provider = IBMProvider(IBM_API_KEY)

# Define a simplified quantum circuit
num_qubits = 7
qc = QuantumCircuit(num_qubits, num_qubits)

# Quantum teleportation setup 
qc.h(0)  # Prepare Qubit 0 in a superposition state
qc. cx(0, 1)  # Entangle Qubit 0 with Qubit 1

# Measure Qubits 0 and 1
qc.measure([0, 1], [0, 1])

# Conditional operation on Qubit 2 based on Qubit 0's measurement
qc.x(2).c_if(qc.clbits[0], 1)  # Apply X-gate on Qubit 2 if Qubit 0 is 1

# Execute the circuit on a quantum computer
backend = provider.get_backend('ibm_nairobi')
transpiled_circuit = transpile(qc, backend=backend)
job = backend. run(transpiled_circuit)
job_monitor(job)

# Retrieve and plot the results
results = job.result().get_counts(qc)
plot_histogram(results)
plt. show()

# Save results and backend information to a JSON file
results_data = {
"results": results,
"backend_info": {
"backend_name": backend. name,
"qubit_count": backend.configuration().n_qubits,
"basis_gates": backend.configuration().basis_gates,
"quantum_volume": backend.configuration().quantum_volume
}
}

file_path = 'c:\\Users\\Documents\\QC\\teleportation_results.json'
with open(file_path, 'w') as file:
json.dump(results_data, file, indent=4)